第三章　AIの歴史と構造：記号処理から学習モデルへ

人工知能は、初期には「記号処理」によって論理的に推論するシステムとして始まり、その後、誤差をもとに内部構造を自律的に調整する「学習モデル」へと進化してきました。
本稿では、現在の生成AIに至るまでの構造的な流れを、時代と技術の両面から整理します。

記号処理型AIの時代（1950〜70年代）

人工知能という概念が正式に定義されたのは、1956年の「ダートマス会議」ですが、1950〜70年代の人工知能研究は「知能とは論理と記号操作で再現できる」という思想に基づいて展開されていました。
当時のコンピュータは処理能力が極めて限られており、大量のデータを直接扱う方式は現実的ではない状況でした。こうした制約の中で、研究者たちは人の思考を論理的な規則の組み合わせとして書き下し、それを機械に実行させることで「人工の知性」を構築しようと試みていたのです。

この時代のAIは、主に次の三つの技術を中心に発展しました。それらはすべて「記号を操作して推論する」という共通の思想に基づいていますが、役割はそれぞれ異なっています。

論理演算

論理演算とは、情報を『IF（条件）–THEN（結果）』の形式で記述し、その条件が『真（true）』か『偽（false）』か を判定して新しい結論を導き出す仕組みを指します。人工知能研究の初期には「知能とは論理的な推論の積み重ねで説明できる」という考え方が広く受け入れられており、この思想に基づいて論理演算が知能の中心的な構造として位置づけられていました。研究者たちは、人の思考を論理規則の集合として書き下し、その規則を機械に実行させることで推論を行わせようとしていたのです。

📝 あらかじめ「親の親は祖父母である」というルールを設定したうえで、次のような条件を入力として与えます

・IF「AはBの親である」
・AND「BはCの親である」

この二つの関係がどちらも true（真） と評価されれば、設定されたルールに従って次の結論が同じく true として導かれます。

・THEN「AはCの祖父母である」

逆に、IF または AND のいずれかが false（偽） と判定された場合、結論は成立せず、THEN は適用されません。
論理演算では、これらの基本的な構造に加えて、条件の選択肢を示す OR、条件を否定する NOT といった演算子も使用されますが、いずれも記号の真偽を組み合わせて結論を導くための形式的な操作に過ぎません。

ここで重要なのは、AIは「親とは何か」「祖父母とは何か」を理解しているわけではなく、「記号間の関係が真か偽かだけを手がかりにして、ルールを適用している」という点です。

真偽の判定が明確に定義されていれば、論理演算は誤りなく推論できますが、現実世界のように「どこまでが親か」「例外はどう扱うか」といった曖昧な状況が混在すると処理が破綻します。また、複雑な領域では、真偽判定そのものが事前に定義できない場合も多く、論理だけで知能を表現することの限界が徐々に明らかになっていきました。

探索アルゴリズム

探索アルゴリズムは、論理演算と並んで記号処理型AIを支えていた基本技術です。
論理演算が「与えられた条件から結論を導く仕組み」であるのに対し、探索アルゴリズムは 「結論に至るための手順そのものを、候補の中から探し出す仕組み」 を担っていました。

記号処理AIの時代には、問題解決を「状態の探索」として捉え、「”どの手順を踏めば目的に到達できるか” を機械的に列挙し、順番に確かめていく」という方法が多くのシステムで採用されていました。

📝 迷路を解く問題は、探索アルゴリズムの典型例です。

迷路の入口を初期状態とし、一歩進むごとに新しい状態が生まれます。
AIは迷路の構造や意味を理解しているわけではなく、「まだ調べていない状態を次に実行する」という手続きだけを決められた順序で実行します。

探索には次のような方法がありますが、どちらも「状態空間を移動する際のルール」が異なるだけです。

・入口に近い状態から順に調べる方法（幅優先探索 – BFS）
・行けるところまで一気に進み、行き止まりで戻る方法（深さ優先探索 – DFS）

探索アルゴリズムは、手順や経路の候補を一つずつ確かめることで「目的地にたどり着く経路」を見つけ出しますが、そこに意味理解や判断は存在しません。

探索アルゴリズムは、論理演算とは異なる角度から記号処理型AIを支えていました。論理演算が「条件が正しければ結論が出る」場面を担当するのに対し、探索は「どの条件や手順を選べば結論に至るのか」という部分を引き受けていたためです。二つの技術は「記号に意味を与えず、形式的な操作だけで問題を扱う」という点で共通しており、記号処理AIはこの組み合わせによって知能を再現しようとしていました。

しかし、探索アルゴリズムにも明確な限界がありました。状態が増えると調べるべき候補が指数的に膨れ上がり、問題が少し複雑になるだけで処理が破綻します。また、探索が扱っているのは「状態の並び」だけであり、その状態が何を意味するのかを理解することはできません。さらに、自然言語のように「状態そのものが事前に定義できない」領域では、探索という枠組み自体が成立しませんでした。

ルールベース推論

ルールベース推論は、記号処理型AIの中心的な技術であり、人間が専門知識を「IF〜THEN」の形式で大量の規則として書き下し、AIがその規則群を参照して結論を導く仕組みです。論理演算が単一の規則に基づいて推論を行うのに対し、ルールベース推論は「多数の規則をどの順番で適用するか」を含めて推論体系を構築する点に特徴があります。
医療診断、装置の故障解析など、専門家が明示的な判断規則を持つ領域で活用されました。

📝 医療診断を例にすると、専門家の判断を次のような形で規則化します。

・IF「発熱がある」 AND「咳が続いている」 THEN「気道感染の疑い」
・IF「気道感染の疑い」 AND「痰の色が濃い」 THEN「細菌性の可能性」
・IF「胸部X線に影」 THEN「肺炎を疑う」

AIは患者のデータを入力として受け取り、その内容に一致する規則を自動的に適用しながら結論を更新していきます。これらの規則は直列に実行されるわけではなく、それぞれ独立した条件として並列に評価されます。入力された情報に一致するルールがあれば、その都度結論が追加されるだけで、規則同士が階段状に結びついているわけではありません。
ここで行われている処理は医学的な意味の理解ではなく、「条件に一致する規則を形式的に適用している」にすぎません。

ルールベース推論は、論理演算や探索アルゴリズムを組み合わせた仕組みとして発展しました。複数の規則の中から「どれを先に適用すべきか」を探索で判断し、規則の条件に一致するかどうかは論理演算で評価します。つまり、記号処理AIが掲げた「知識を記号として表し、規則を適用すれば知能を再現できる」という思想を最も直接的な形で具現化したのがルールベース推論でした。

しかし、この方式にも構造的な限界がありました。現実の領域では例外や曖昧な症状が多く、すべてを「IF〜THEN」で記述することが不可能になります。規則が増えるほど矛盾や衝突も発生しやすく、どの規則を優先すべきかを人が事前に決めておく必要がありました。また、規則に書かれていないケースに遭遇すると AIは結論を導けず、未知の状況に柔軟に対応することもできません。

ルールベース推論は専門領域で一定の成果を上げましたが、日常的で曖昧な問題には適用できず、「知識をすべて記号化する」という方針そのものの限界が次第に明らかになっていきました。

ニューラルネットワークの停滞と発展

人間の脳の仕組みを参考にした人工ニューロンのモデルは、すでに1943年にマカロックとピッツによって提案されており、「知能を多数の単純な要素の組み合わせとして再現する」という発想そのものは当初から存在していました。しかし、当時のモデルは計算能力や学習手法の制約が大きく、理論的な可能性が示されながらも実用化には至らず、その後の研究の主流は記号処理へと移っていきました。

1980年代以降、記号処理だけでは現実世界の曖昧で例外の多い問題に対応できないことが明らかになるにつれ、「知能を固定した規則で表す」方式の限界が顕在化していきます。この状況の中で、脳のように多数の要素が並列に動作し、誤差に応じて内部構造が変化するモデルとしてニューラルネットワークが再び注目されるようになりました。

研究者たちは、人間の脳が持つ「刺激と誤差に応じてつながりを変化させる」という特性に着目し、知能を明示的な規則ではなく「データから自律的に形成される構造」として捉え直そうとしました。コンピュータの処理能力は依然として限られていたものの、こうした発想の転換により、ニューラルネットワークは「記号を操作して推論するAI」とは異なる、新しい方向性として再びAI研究の中心に据えられていったのです。

パーセプトロン

パーセプトロンは、1958年にフランク・ローゼンブラットによって提案された、人工ニューロンを組み合わせた初期の学習モデルです。これは、人の脳が「多数の神経細胞が刺激に応じて反応し、そのつながり方が経験によって変化する」という仕組みを参考にし、データから規則を学習する仕組みを持つモデルとして登場しました。
記号処理型AIがすべての知識をあらかじめルールとして書き下していたのに対し、パーセプトロンは「正解との違い」を手がかりに、自動的に内部構造を調整できる点で大きく異なっていました。

📝 手書き数字認識の初期研究では、数字の「5」を白黒の小さなマス目にした図を用意し、「黒い部分がどこにどれくらいあるか」を手がかりに、パーセプトロンに「これは ‘5’ かどうか」を学習させる、という試みが行われていました。

モデルは、判断を誤った場合に「重み」と呼ばれる内部パラメータを少しずつ更新し、次の判断で誤差が小さくなるよう調整します。専門家がルールを細かく設計しなくても、データを繰り返し見せることで性能を向上させられる可能性が示されました。

ただし、この時点でのパーセプトロンには明確な限界がありました。
扱えるのは「直線1本で分類できる単純な問題（線形分離可能な問題）」に限られており、複雑なパターンや例外を含むデータには対応できなかったのです。
この限界は、後に象徴的な例として扱われる「XOR問題」で強く浮き彫りになります。

パーセプトロンは、記号処理とは異なるアプローチで人工知能の可能性を広げましたが、その限界を克服するには「中間層を持つ多層構造」と「中間層を学習させる方法」が必要でした。これは1986年に誤差逆伝播法が提案されるまで実現せず、研究は一時的に停滞することになります。

線形分離

パーセプトロンが高い期待を集めた一方で、その能力には「構造的な限界」がありました。
それが「線形分離」と呼ばれる性質です。
線形分離とは、データを分類するときに「1 本の直線（または平面）で区切れる場合にしか正しく判断できない」という制約を指します。

この性質は、パーセプトロンの内部構造そのものに由来しています。
モデルは、入力された情報を「重み」と呼ばれる数値でまとめあげ、最後に「境界」を 1 本だけ引くようなしくみで判断を行います。
そのため、境界が直線で表せる問題ならうまく分類できますが、より複雑な形の境界が必要な場合には対応できません。

📝 図形を分類する場面を想定します。

・左側に丸い印
・右側に四角い印

このような配置であれば、丸と四角の間に直線を 1 本引くだけで分類できるため、パーセプトロンで対応できます。
しかし、データの配置が「丸を囲むように四角が配置されている」といった複雑な状況になると、直線 1 本で分類することはできません。
丸を囲む四角を分けるには「曲線」や「複数の境界線」が必要ですが、パーセプトロンの構造ではこのような複雑な境界を作り出すことができません。

この限界は、単に性能が低いという問題ではなく、「モデルの原理そのものが複雑な分類問題に対応できない」ことを意味していました。

記号処理型AIでは、ルールが足りなければ人が追加すればよかったのですが、パーセプトロンでは内部構造を自動調整する仕組みが導入されたことで、「そもそも構造的に表現できない問題」が存在するという事実がより深刻な障害となりました。

この線形分離の制約は、研究の次の段階で象徴的な例として取り上げられる「XOR問題」で決定的になります。
線形分離ができない問題に対してパーセプトロンがどうしても正答できないことが示され、ニューラルネットワーク研究は大きく停滞していくことになります。

XOR問題

パーセプトロンの限界を決定的に示した問題として、しばしば取り上げられるのが「XOR（排他的論理和）問題」です。
XORとは「どちらか一方だけが真なら真、両方が真または両方が偽なら偽」という論理のことを指します。

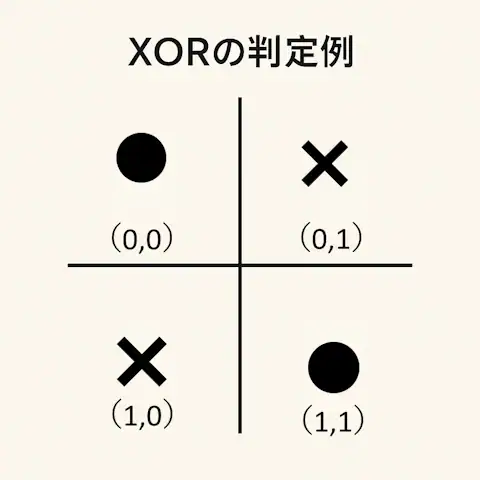
パーセプトロンは「直線 1 本で分類できる問題（線形分離可能な問題）」にしか対応できない構造を持っていたため、XORのような「非線形」の問題は原理的に解くことができませんでした。

この限界は、1969年にマービン・ミンスキーとシーモア・パパートが、著書『Perceptrons』で数学的に示したことで強く認識されるようになり、「パーセプトロンは学習によって何でも解けるようになる」という見方は大幅に後退しました。

XOR問題が象徴的だった理由は、「判断が複雑だから解けない」のではなく、「モデルの構造そのものが原因で、原理的に解けない」と示された点にあります。
研究者たちは XOR問題から、「より複雑な境界を作るには、中間層（隠れ層）を持つ多層ネットワークが必要である」ことを理解していましたが、中間層を「どうやって学習させるのか」という方法が確立しておらず、複雑な構造を設計しても学習が成立しないという根本的な問題の壁に突き当たります。

その結果、ニューラルネットワーク研究は長い停滞期に入ります。
研究の焦点は再び記号処理型AIへと戻り、「学習によって知能を獲得するモデル」という発想は一時的に後退していきました。

誤差逆伝播法（バックプロパゲーション）

1986年、Rumelhart、Hinton、Williams らによって提案された「誤差逆伝播法（バックプロパゲーション）」によって、隠れ層を含む多層ネットワークが初めて「学習可能な構造」として成立し、ニューラルネットワーク研究は再び進展し始めます。

ニューラルネットワークは多数の「ノード（人工ニューロン）」で構成されています。
「ノード」はニューラルネットワークを構成する最小の処理単位です。
複数の入力を受け取り、それぞれに「重み」という重要度を掛け合わせて合計し、その値が一定の閾値を超えたかどうかで出力を決める、小さな判断装置のような役割を持っています。

例えば、迷惑メールの判定では、「お金」「当選」「急ぎ」などの語が含まれているかどうかを数値化し、それぞれに重みを掛け合わせて合計します。
この合計が閾値を超えれば「迷惑メール」、超えなければ「通常メール」と判断する仕組みです。ノードは語の意味を理解しているわけではなく、単に数値を合計して基準値と比較するだけの処理を行っています。

誤差逆伝播法は、モデルが出した出力がどれくらい正解と違っていたか（誤差）を計算し、その誤差を 出力側から入力側へ向かって逆向きに伝えることで、各ノードの重みを少しずつ調整する方法です。

通常メールと判定したメールが実際には迷惑メールだった場合、誤差逆伝播法によって「お金」「当選」「急ぎ」などのキーワードに対応する重みが、迷惑メール方向へ調整されます。
この調整を繰り返すことで、多層ネットワークはより複雑なパターンを捉えられるようになり、単層パーセプトロンでは扱えなかった非線形問題にも対応できるようになります。
また、「重み」は学習開始時点では小さなランダム値から始まり、学習を重ねるうちに、モデル自身がどの入力をどれだけ重視すべきかを自動的に調整していきます。問題が複雑になるほど、モデルが扱う情報も増えるため、それに対応して必要な重みの数も自然に増えていきます。こうした重みの最適化はすべて誤差逆伝播法によって行われ、モデルは試行錯誤を通じて出力の精度を高めていきます。

誤差逆伝播法によって、単層パーセプトロンでは不可能だった XOR問題のような非線形問題についても、多層ネットワークであれば学習が可能になりました。
これは「単層パーセプトロンの限界は多層構造で克服できる」という事実を具体的に示した転換点であり、この仕組みが実用化されたことで、多層ネットワークは初めて本格的に学習可能なモデルとして成立し、ニューラルネットワーク研究は再び活発化していきます。

深層学習の確立と自然言語処理への展開

誤差逆伝播法によって学習可能になった多層ネットワークとは、多数の「ノード（人工ニューロン）」が階層状に連なり、前の層の出力を次の層が受け取りながら情報を段階的に変換していく構造をもっています。しかし1980〜90年代当時、このネットワークを深く重ねることは現実的ではありませんでした。層を増やすほど計算量が急激に膨らみ、当時の処理能力では深い構造を十分に学習させることが難しかったためです。

この時期のニューラルネットワークでは、入力データから何を判断材料として抽出すべきかをモデル自身に任せることができず、「特徴量設計」と呼ばれる作業が不可欠でした。画像認識であれば輪郭や角度、音声処理であれば周波数成分といったように、人間があらかじめ有効だと考える特徴を定義し、その値をモデルに入力する必要がありました。
多層構造が理論的には学習可能になっていたとしても、「どの特徴を学習に使うか」という核心部分は依然として人間側が設計しなければならず、モデルが生データから自律的に判断基準を獲得する段階には達していませんでした。

1990年代後半から2000年代にかけて、CPUや GPUの性能向上よって多層ネットワークを深く構築しても学習させられるだけの処理能力が確保され、同時にインターネットの普及や標準化されたデータセットの公開、大容量ストレージの低価格化など、大規模データを扱える環境も整い始めました。こうした基盤が組み合わさったことで、ネットワークは入力データの細かな部分からパターンを見つけ出し、より本質的な特徴へと段階的に変換する処理を自動で行えるようになり、「深層学習（ディープラーニング）」が現実的な方法として成立していきます。
深層化したモデルは、人間が事前に指定していない特徴まで自律的に学習できるようになり、従来の手作業による特徴量設計への依存は徐々に薄れていきました。

時間を扱うモデル：RNNとLSTM

文章や音声のように「順番や時間的な流れが意味に強く影響するデータ」を扱うために登場したのが、再帰型ニューラルネットワーク（RNN）です。
画像のように一枚ごとに独立した情報を処理するモデルとは異なり、RNNは「ひとつ前の状態」を内部に保持しながら次の入力を処理する構造を備えていました。

これは、人が文章を読むときに、直前の文や単語の記憶を保持しながら理解を進める働きに近い仕組みです。RNNは入力された語ごとに内部状態（隠れ状態）を更新し、その情報を次の処理に連続的に引き渡すことで、文脈に応じた判断を可能にしようとしたのです。

📝 文章の途中で「その後、彼は走り出した」と書かれていた場合、「その後」が何を指しているかは、前に出てきた出来事に依存しています。RNNは、前の入力によって内部状態（数値）が更新され、その数値が次の処理に影響するという仕組みを持っており、その内部状態の更新ルールは誤差逆伝播による学習によって最適化されます。

RNNはそれまで扱いにくかった「時間方向の依存関係」を捉える手段を提供し、翻訳、音声認識、文章分類などの分野で重要な役割を果たし始めました。
しかし、文章が長くなるにつれて冒頭の情報が内部で徐々に薄れ、重要な文脈が失われていく「勾配消失問題」と呼ばれる構造的制約によって、RNNでは長い文脈を維持したまま処理することが困難になるという実用上の限界がありました。

この限界を補うために登場したのが、1997年に提案された「LSTM（Long Short-Term Memory：長短期記憶）」 です。LSTMは、RNNの内部に「どの情報を残すか」「どの情報を捨てるか」を選び取る仕組み（ゲート機構）を追加した構造を持っています。

📝 LSTMは、重要な情報を「メモに残し」、不要な情報を「その場で忘れる」ような動作を自動的に行います。これにより、文章の冒頭で提示された文脈や特徴を、終わりのほうまで保持しながら処理できるようになりました。
ただし、この保持や忘却の判断は意味を理解して行われているのではなく、RNNと同様に誤差逆伝播によって最適化された数値パターンに従っているだけです。

LSTMの導入によって、長文の翻訳、音声の連続認識、チャット文脈の保持など、従来は扱いづらかった問題にも現実的に対応できるようになり、自然言語処理の性能は大きく向上します。しかし、LSTMにも計算の重さや並列処理の難しさといった制約は残っており、長文処理には依然として限界がありました。

文脈処理の転換：AttentionとTransformer

RNNと LSTMは、時間に沿って連続するデータを扱うための有効な手段を提供しましたが、文章が長くなるほど計算が重くなる構造的な制約があり、並列処理が困難であることが大きな課題として残っていました。こうした限界を根本から乗り越える新しい仕組みとして提案されたのが、「Attention（注意機構）」です。

Attentionは、文章中の単語同士が「どれくらい関連しているか」を数値として計算し、その関連度に応じて情報の重要度を自動的に調整する仕組みです。RNNが順番どおりにしか処理できなかったのに対し、Attentionは必要な箇所を直接参照して処理できる点が決定的に異なっていました。

📝文章に「その問題は解決した」と書かれている場合、「その」が実際に指している対象は、この文より前に登場した別の語句にあります。Attentionは、文中のすべての語に対して「どの語をどれだけ参照すべきか」という統計的な関連度（重み）を計算し、関連度が最も高い語を参照対象として扱います。
そのため、「その」が前文の「生成AI」という語と最も強く関連づけられる場合、モデルは次の処理で「その」が「生成AI」を参照すべきものとして扱います。ここで行われているのは語の意味理解ではなく、参照の強弱を数値で調整しているだけの処理です。

Attentionが登場したことで、文章全体を並列に処理できるようになり、文のどの位置にある情報でも直接参照できるようになりました。これは、長文処理における構造的な制約を大きく緩和し、従来の RNN・LSTM を基盤としたモデルでは困難だった大規模な言語処理を可能にする重要な転換点でした。

この Attention の仕組みを全面的に採用し、モデル全体を Attention のみで構成することで、文章全体を一括して計算できるようにしたのが Transformer です。Transformer は深さや幅を拡張しても計算を完全に並列化でき、モデルの拡張性が飛躍的に向上しました。
ここでいう「並列」とは、文章を順番どおりに１語ずつ処理するのではなく、すべての語の関係を一括で計算できる構造（GPUの行列演算） を指します。

📝 Transformer は、「自己注意機構（Self-Attention）」を複数段重ねることで、入力文の内部で生じるさまざまな関連性を段階的に抽出する構造を持っています。単語の位置情報は「位置エンコーディング」という数値表現で補い、文章の順序を失わずに並列処理を行っています。

Transformerの構造は、単語間の関連を段階的に集約することで文章全体のパターンを高精度に捉えることができ、翻訳、要約、質問応答など多様な自然言語処理タスクで従来モデルを大きく上回る性能を示しました。さらに、ネットワークの深さや幅を増やしても性能が伸びやすく、学習データを大規模化するほど能力が向上する特性を持っていたため、この構造を基盤にした「大規模言語モデル（LLM）」が開発されていくことになります。

AIリテラシー：AIの限界と誤解 シリーズ一覧

更新履歴